Đề thi thử giữa học kỳ 2 môn Toán lớp 10 online - Mã đề 02

Danh sách câu hỏi

1. Câu 1:

   Cho hàm số $y=f\left( x \right)=a{{x}^{2}}+bx+c$ có đồ thị như hình bên. Dấu của hệ số $a$ và biệt thức $\text{ }\!\!\Delta\!\!\text{ }$ là

   

   • A. $a>0,\text{ }\!\!\Delta\!\!\text{ }>0$.
   • B. $a<0,\,\Delta >0$.
   • C. $a<0,\,\Delta >0$.
   • D. $a<0,\text{ }\!\!\Delta\!\!\text{ }=0$.

2. Câu 2:

   Bất phương trình nào sau đây có tập nghiệm là $S=\mathbb{R}\setminus \left\{ 2 \right\}$ ?

   • A. ${{x}^{2}}+4x+5\le 0$.
   • B. $-2{{x}^{2}}+5x-11>0$.
   • C. $-3{{x}^{2}}+12x-12<0$.
   • D. $-3{{x}^{2}}+12x-12\ge 0$.

3. Câu 3:

   Giá trị của tham số $m$ để phương trình ${{x}^{2}}-\left( m+1 \right)x+4=0$ có nghiệm là

   • A. $\left( -5;3 \right)$.
   • B. $\left( -\infty ;-5\left] \cup  \right[3;+\infty  \right)$.
   • C. $\left[ -5;3 \right]$.
   • D. $\left( -\infty ;-5 \right)\cup \left( 3;+\infty  \right)$.

4. Câu 4:

   Cho tam thức bậc hai $f\left( x \right)=m{{x}^{2}}+2x+m$. Giá trị của tham số $m$ để $f\left( x \right)\ge 0, \forall x\in \mathbb{R}$ là

   • A. $m\ge 1$.
   • B. $m>1$.
   • C. $m>0$.
   • D. $m < 2$.

5. Câu 5:

   Cho bất phương trình $-{{x}^{2}}-2mx+{{m}^{2}}-2m\le 0$. Giá trị của $m$ để bất phương trình có nghiệm đúng với mọi $x\in \mathbb{R}$ là

   • A. $0\le m\le 1$.
   • B. $0 < m < 1$.
   • C. $1\le m\le 2$.
   • D. $1 < m < 2$.

6. Câu 6:

   Tập nghiệm của bất phương trình $\frac{2{{x}^{2}}-3x+4}{{{x}^{2}}+2}>1$ là

   • A. $\left( -\infty ;-1 \right)\cup \left( 2;+\infty  \right)$.
   • B. $\left( -\infty ;-2 \right)\cup \left( -1;+\infty  \right)$.
   • C. $\left( -\infty ;1 \right)\cup \left( 2;+\infty  \right)$.
   • D. $\left( -\infty ;2 \right)\cup \left( 4;+\infty  \right)$.

7. Câu 7:

   Tam thức bậc hai $f\left( x \right)=-{{x}^{2}}+5x-6.f\left( x \right)>0$ khi và chỉ khi

   • A. $x\in \left( -\infty ;2 \right)$.
   • B. $\left( 3;+\infty  \right)$.
   • C. $x\in \left( 2;+\infty  \right)$.
   • D. $x\in \left( 2;3 \right)$.

8. Câu 8:

   Số giá trị nguyên của $x$ để $2{{x}^{2}}-7x-9<0$ là

   • A. 3.
   • B. 4.
   • C. 5.
   • D. 6.

9. Câu 9:

   Bảng xét dấu nào sau đây là của tam thức $f\left( x \right)=-{{x}^{2}}+4x-4$ ?

   • A.
   • B.
   • C.
   • D.

10. Câu 10:

    Tìm tập nghiệm của hệ bất phương trình $\left\{ \begin{array}{*{35}{l}} {{x}^{2}}-4x+3>0 \\ {{x}^{2}}-6x+8>0 \\\end{array} \right..$

    • A. $\left( -\infty ;1 \right)\cup \left( 3;+\infty  \right)$.
    • B. $\left( -\infty ;1 \right)\cup \left( 4;+\infty  \right)$.
    • C. $\left( -\infty ;2 \right)\cup \left( 3;+\infty  \right)$.
    • D. $\left( 1;4 \right)$.

11. Câu 11:

    Cho bất phương trình ${{x}^{2}}+4x+\left| x+2 \right|-m\le 0$. Xác định $m$ để bất phương trình có nghiệm.

    • A. $-\frac{17}{4}\le m\le -4$.
    • B. $m\le -4$.
    • C. $m\ge -\frac{17}{4}$.
    • D. $m\ge -4$.

12. Câu 12:

    Cho phương trình $\left( m-5 \right){{x}^{2}}+2\left( m-1 \right)x+m=0$ (1). Với giá trị nào của $m$ thì (1) có 2 nghiệm ${{x}_{1}},{{x}_{2}}$ thỏa ${{x}_{1}}<1<{{x}_{2}}$ ?

    • A. $m\ge 5$.
    • B. $m<\frac{7}{4}$.
    • C. $\frac{7}{4}<m<5$.
    • D. $\frac{7}{4}\le m\le 5$.

13. Câu 13:

    Điều kiện xác định của phương trình $\sqrt{x-1}+\sqrt{x-2}=\sqrt{x-3}$ là:

    • A. $\left( 3;+\infty  \right)$.
    • B. $\left[ 2;+\infty  \right)$.
    • C. $\left[ 1;+\infty  \right)$.
    • D. $\left[ 3;+\infty  \right)$.

14. Câu 14:

    Phương trình sau có bao nhiêu nghiệm $\sqrt{x}=\sqrt{-x}$ ?

    • A. 0.
    • B. 1.
    • C. 2.
    • D. Vô số.

15. Câu 15:

    Tập nghiệm của phương trình $x-\sqrt{x-3}=\sqrt{3-x}+3$ là:

    • A. $S=\varnothing $.
    • B. $S=\left\{ 3 \right\}$.
    • C. $S=\left[ 3;+\infty  \right)$.
    • D. $S=\mathbb{R}$.

16. Câu 16:

    Phương trình $\sqrt{f\left( x \right)}=\sqrt{g\left( x \right)}$ tương đương với phương trình nào sau đây?

    • A. $f\left( x \right)=g\left( x \right)$.
    • B. ${{f}^{2}}\left( x \right)={{g}^{2}}\left( x \right)$.
    • C. $\left[ \begin{array}{*{35}{l}} f\left( x \right)\ge 0 \\ f\left( x \right)=g\left( x \right) \\\end{array} \right..$
    • D. $\left\{ \begin{array}{*{35}{l}} f\left( x \right)\ge 0 \\ f\left( x \right)=g\left( x \right) \\\end{array} \right.$

17. Câu 17:

    Phương trình ${{(x-4)}^{2}}=x-2$ là phương trình hệ quả của phương trình nào sau đây?

    • A. $x-4=x-2$.
    • B. $\sqrt{x-2}=x-4$.
    • C. $\sqrt{x-4}=\sqrt{x-2}$.
    • D. $\sqrt{x-4}=x-2$.

18. Câu 18:

    Số giá trị nguyên của $m$ để phương trình $\sqrt{{{x}^{2}}-x+m}=\sqrt{x-3}$ có hai nghiệm phân biệt là

    • A. 0.
    • B. 1.
    • C. 2.
    • D. 3.

19. Câu 19:

    Trong mặt phẳng toạ độ $Oxy$, cho $\vec{a}=\left( -4;2 \right),\vec{b}=\left( 2k;-k \right)$. Với giá trị nào của $k$ dưới đây thì $\vec{a}=\vec{b}?$

    • A. $k=-\frac{1}{2}$.
    • B. $k=2$.
    • C. $k=-2$.
    • D. Không tồn tại $k$.

20. Câu 20:

    Trong mặt phẳng toạ độ $Oxy$, cho $\vec{a}=\left( -m+2n;-1 \right),\vec{b}=\left( 5;-m-n \right)$. Với giá trị nào của $m,n$ dưới đây thì $\vec{a}=\vec{b}$ ?

    • A. $m=-1,n=2$.
    • B. $m=2,n=-1$.
    • C. $m=2,n=1$.
    • D. Không tồn tại $m,n$.

21. Câu 21:

    Trong mặt phẳng toạ độ $Oxy$, cho $A\left( 2;-3 \right),B\left( -4;1 \right)$ và $C\left( -1;-1 \right)$. Khẳng định nào dưới đây là đúng?

    • A. $\overrightarrow{AB}=2\overrightarrow{AC}$.
    • B. $\overrightarrow{AB}=\frac{1}{2}\overrightarrow{AC}$.
    • C. $\overrightarrow{AB}=-2\overrightarrow{AC}$
    • D. $\overrightarrow{AB}=-\frac{1}{2}\overrightarrow{AC}$.

22. Câu 22:

    Trong mặt phẳng toạ độ $Oxy$, cho đường thẳng $d:\left\{ \begin{array}{*{35}{l}} x=-2-t \\ y=4+3t \\\end{array} \right.$.Trong các vectơ sau, vectơ nào là vectơ chỉ phương của $d$ ?

    • A. $\vec{u}=\left( -2;4 \right)$.
    • B. $\vec{v}=\left( 3;1 \right)$.
    • C. $\vec{m}=\left( -1;-3 \right)$.
    • D. $\vec{n}=\left( -1;3 \right)$.

23. Câu 23:

    Trong mặt phẳng toạ độ $Oxy$, cho đường thẳng $\text{ }\!\!\Delta\!\!\text{ }:x-3y-2=0$. Trong các vectơ sau, vectơ nào là vectơ pháp tuyến của $\text{ }\!\!\Delta\!\!\text{ }$ ?

    • A. $\vec{u}=\left( -3;1 \right)$.
    • B. $\vec{v}=\left( 3;1 \right)$.
    • C. $\vec{m}=\left( -1;-3 \right)$.
    • D. $\vec{n}=\left( 1;-3 \right)$.

24. Câu 24:

    Trong mặt phẳng toạ độ $Oxy$, cho đường thẳng $\text{ }\!\!\Delta\!\!\text{ }:-x+2y-2=0$. Trong các vectơ sau, vectơ nào là vectơ chỉ phương của $\text{ }\!\!\Delta\!\!\text{ }$ ?

    • A. $\vec{u}=\left( -1;2 \right)$.
    • B. $\vec{v}=\left( -2;-1 \right)$.
    • C. $\vec{m}=\left( -2;1 \right)$.
    • D. $\vec{n}=\left( 1;2 \right)$.

25. Câu 25:

    Trong mặt phẳng toạ độ $Oxy$, cho đường thẳng $d:\left\{ \begin{array}{*{35}{l}} x=-2t \\ y=4+t. \\\end{array} \right.$ Trong các vectơ sau, vectơ nào là vectơ pháp tuyến của $d$ ?

    • A. $\vec{u}=\left( -2;1 \right)$.
    • B. $\vec{v}=\left( 2;-1 \right)$.
    • C. $\vec{m}=\left( 1;-2 \right)$.
    • D. $\vec{n}=\left( 1;2 \right)$.

26. Câu 26:

    Đường thẳng đi qua $A\left( -3;2 \right)$ và nhận $\vec{n}=\left( 1;5 \right)$ làm vectơ pháp tuyến có phương trình tổng quát là:

    • A. $x+5y+7=0$.
    • B. $-x+5y-13=0$.
    • C. $-5x+y-17=0$.
    • D. $x+5y-7=0$.

27. Câu 27:

    Phương trình tham số của đường thẳng $d$ đi qua $A\left( 0;-2 \right)$ và có vectơ chỉ phương $\vec{u}=\left( 2;-3 \right)$ là:

    • A. $\left\{ \begin{array}{*{35}{l}} x=2t \\ y=-2-3t \\\end{array} \right.$
    • B. $\left\{ \begin{array}{*{35}{l}} x=2 \\ y=-3-2t \\\end{array} \right.$
    • C. $\left\{ \begin{array}{*{35}{l}} x=3t \\ y=3+2t \\\end{array} \right.$
    • D. $\left\{ \begin{array}{*{35}{l}} x=2+t \\ y=-3-2t \\\end{array} \right.$

28. Câu 28:

    Phương trình tham số của đường thẳng $d:\frac{x}{4}-\frac{y}{3}=1$ là:

    • A. $\left\{ \begin{array}{*{35}{l}} x=4+3t \\ y=4t \\\end{array} \right.$
    • B. $\left\{ \begin{array}{*{35}{l}} x=4-4t \\ y=3t \\\end{array} \right.$
    • C. $\left\{ \begin{array}{*{35}{l}} x=4+4t \\ y=3t \\\end{array} \right.$
    • D. $\left\{ \begin{array}{*{35}{l}} x=4-3t \\ y=4t \\\end{array} \right.$

29. Câu 29:

    Góc giữa hai đường thẳng ${{\text{ }\!\!\Delta\!\!\text{ }}_{1}}:-2x+y-7=0$ và ${{\text{ }\!\!\Delta\!\!\text{ }}_{2}}:\left\{ \begin{array}{*{35}{l}} x=2-t \\ y=1+3t\text{. }\!\!~\!\!\text{ } \\\end{array} \right.$ là

    • A. ${{30}^{\circ }}$.
    • B. ${{45}^{\circ }}$.
    • C. ${{60}^{\circ }}$.
    • D. ${{90}^{\circ }}$.

30. Câu 30:

    Trong mặt phẳng toạ độ, cho ba điểm $A,B,C$ và đường thẳng $\text{ }\!\!\Delta\!\!\text{ }$ đi qua hai điểm $A,B$ (xem hình bên). Khoảng cách từ $C$ đến đường thẳng $\text{ }\!\!\Delta\!\!\text{ }$ là bao nhiêu?

    

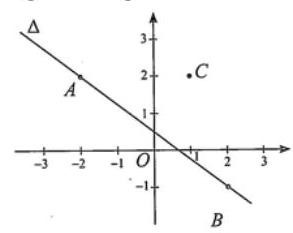
    • A. $\frac{5}{9}$.
    • B. $\frac{9}{5}$.
    • C. $\frac{8}{5}$.
    • D. $\frac{4}{5}$.

31. Câu 31:

    Cho đường thẳng $d:3x-2y+1=0$ và điểm $M\left( 1;2 \right)$. Phương trình đường thẳng $\text{ }\!\!\Delta\!\!\text{ }$ qua $M$ và tạo với $d$ một góc ${{45}^{\circ }}$ là

    • A. $2x-y=0$ và $5x+y-7=0$.
    • B. $x-5y+9=0$ và $3x+y-5=0$.
    • C. $3x-2y+1=0$ và $5x+y-7=0$.
    • D. $x-5y+9=0$ và $5x+y-7=0$.

32. Câu 32:

    Khoảng cách từ $O\left( 0;0 \right)$ đến đường thẳng $\text{ }\!\!\Delta\!\!\text{ }:4x-3y-5=0$ là

    • A. $-5$.
    • B. $0$.
    • C. $1$.
    • D. $\frac{1}{5}$.

33. Câu 33:

    Trong mặt phẳng toạ độ, đường tròn tâm $I\left( 3;-1 \right)$ và bán kính $R=2$ có phương trình là

    • A. ${{(x+3)}^{2}}+{{(y-1)}^{2}}=4$.
    • B. ${{(x-3)}^{2}}+{{(y-1)}^{2}}=4$.
    • C. ${{(x-3)}^{2}}+{{(y+1)}^{2}}=4$.
    • D. ${{(x+3)}^{2}}+{{(y+1)}^{2}}=4$.

34. Câu 34:

    Phương trình đường tròn tâm $I\left( 3;-2 \right)$ và đi qua điểm $M\left( -1;1 \right)$ là

    • A. ${{(x+3)}^{2}}+{{(y-2)}^{2}}=5$.
    • B. ${{(x-3)}^{2}}+{{(y+2)}^{2}}=25$.
    • C. ${{(x-3)}^{2}}+{{(y+2)}^{2}}=5$.
    • D. ${{(x-3)}^{2}}+{{(y-2)}^{2}}=25$.

35. Câu 35:

    Phương trình đường tròn có đường kính $AB$ với $A\left( -1;2 \right)$ và $B\left( 3;2 \right)$ là

    • A. ${{(x+1)}^{2}}+{{(y+2)}^{2}}=4$.
    • B. ${{(x+1)}^{2}}+{{(y-2)}^{2}}=16$.
    • C. ${{(x-1)}^{2}}+{{(y-2)}^{2}}=4$.
    • D. ${{(x-3)}^{2}}+{{(y-2)}^{2}}=16$.