Đề thi thử THPT QG năm 2021 môn Toán online - Đề thi của Trường THPT Chuyên Long An lần 3

Thi thử THPT quốc gia môn Toán online - Đề thi của Trường THPT Chuyên Long An lần 3. Có chấm điểm tự động kèm đáp án chi tiết.

Thí sinh đọc kỹ đề trước khi làm bài.

Câu 1:

Câu 1:

Có hai bút chì màu, các bút chì khác nhau. Hộp thứ nhất có 5 bút chì màu đỏ và 7 bút chì màu xanh. Hộp thứ hai có 8 bút chì đỏ và 4 bút chì màu xanh. Chọn ngẫu nhiên mỗi hộp một cây bút chì. Xác suất để có 1 cây bút chì màu đỏ và 1 cây bút chì màu xanh là:

A. $\frac{17}{36}.$

B. $\frac{7}{12}.$

C. $\frac{19}{36}.$

D. $\frac{5}{12}.$

Câu 2:

Câu 2:

Cho hình chóp $S.ABC$ có $SA\bot \left( ABC \right)$ và $AB\bot BC.$ Góc giữa hai mặt phẳng (SBC) và (ABC) là góc nào sau đây?

A. $\angle SCA$

B. $\angle SIA$ với I là trung điểm của BC.

C. $\angle SCB$

D. $\angle SBA$

Câu 3:

Câu 3:

Một hộp đựng 40 tấm thẻ được đánh số thứ tự từ 1 đến 40. Rút ngẫu nhiên 10 tấm thẻ. Tính xác suất để lấy được 5 tấm thẻ mang số lẻ và 5 tấm thẻ mang số chẵn, trong đó có đúng một thẻ mang số chia hết cho 6.

A. $\frac{126}{1147}$

B. $\frac{252}{1147}$

C. $\frac{26}{1147}$

D. $\frac{12}{1147}$

Câu 4:

Câu 4:

Trong bài thi thực hành huấn luyện quân sự có một tình huống chiến sĩ phải bơi qua một sông để tấn công mục tiêu ở ngay phía bờ bên kia sông. Biết rằng lòng sông rộng 100m và vận tốc bơi của chiến sĩ bằng một phần ba vận tốc chạy trên bộ. Hãy cho biết chiến sĩ phải bơi bao nhiêu mét để đến được mục tiêu nhanh nhất? Biết dòng sông là thẳng, mục tiêu cách chiến sĩ 1km theo đường chim bay và chiến sĩ cách bờ bên kia 100m.

A. $\frac{200\sqrt{2}}{3}\left( m \right)$

B. $60\sqrt{5}\left( m \right)$

C. $\frac{200\sqrt{3}}{3}\left( m \right)$

D. $75\sqrt{2}\left( m \right)$

Câu 5:

Câu 5:

Cho hàm số $y=a{{x}^{4}}+b{{x}^{2}}+c$ có đồ thị như hình vẽ bên.

Mệnh đề nào dưới đây đúng?

A. $a<0,b<0,c<0$

B. $a<0,b>0,c<0$

C. $a>0,b<0,c<0$

D. $a>0,b<0,c>0$

Câu 6:

Câu 6:

Cho hình chóp S.ABCD đáy là hình chữ nhật có $AB=2a\sqrt{3},AD=2a.$ Mặt bên (SAB) là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Thể tích khối chóp S.ABD là:

A. $4\sqrt{3}{{a}^{3}}$

B. $4{{a}^{3}}$

C. $2\sqrt{3}{{a}^{3}}$

D. $\frac{2\sqrt{3}}{3}{{a}^{3}}$

Câu 7:

Câu 7:

Có bao nhiêu số có ba chữ số đôi một khác nhau mà các chữ số đó thuộc tập hợp $\left\{ 1;2;3;...;9 \right\}?$

A. ${{9}^{3}}$

B. ${{3}^{9}}$

C. $A_{9}^{3}$

D. $C_{9}^{3}$

Câu 8:

Câu 8:

Cho đồ thị hàm số $y=\frac{\sqrt{4-{{x}^{2}}}}{{{x}^{2}}-3x-4}$ có tất cả bao nhiêu đường tiệm cận?

A. 0

B. 3

C. 2

D. 1

Câu 9:

Câu 9:

Tìm tất cả các giá trị của tham số $a$ để đồ thị hàm số $y=\frac{{{x}^{2}}+2}{{{x}^{3}}+a{{x}^{2}}}$ có 3 đường tiệm cận.

A. $a>0$

B. $a<0,a\ne \pm 1$

C. $a\ne 0,a\ne \pm 1.$

D. $a\ne 0$

Câu 10:

Câu 10:

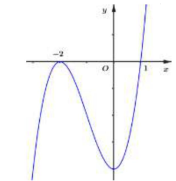
Cho hàm số $y=f\left( x \right)$ có đạo hàm liên tục trên $\mathbb{R}$ và có đồ thị hàm số $y=f'\left( x \right)$ như hình vẽ bên dưới. Xét hàm số $g\left( x \right)=f\left( {{x}^{2}}-3 \right)$ và các mệnh đề sau:

I. Hàm số $g\left( x \right)$ có 3 điểm cực trị.

II. Hàm số $g\left( x \right)$ đạt cực tiểu tại $x=0.$

III. Hàm số $g\left( x \right)$ đạt cực đại tại $x=2.$

IV. Hàm số $g\left( x \right)$ đồng biến trên khoảng $\left( -2;0 \right)$.

V. Hàm số $g\left( x \right)$ nghịch biến trên khoảng $\left( -1;1 \right).$

Có bao nhiêu mệnh đề đúng trong các mệnh đề trên?

A. 3

B. 2

C. 4

D. 1

Câu 11:

Câu 11:

Đồ thị hàm số $y=\frac{{{x}^{4}}}{2}-{{x}^{2}}+3$ có mấy điểm cực trị

A. 3

B. 2

C. 0

D. 1

Câu 12:

Câu 12:

Khoảng cách giữa hai điểm cực của đồ thị hàm số $y=-{{x}^{3}}+3x+2$ bằng:

A. $2\sqrt{5}$

B. $2\sqrt{3}$

C. $3\sqrt{5}$

D. 2

Câu 13:

Câu 13:

Có tất cả 120 các chọn 3 học sinh từ nhóm n (chưa biết) học sinh. Số n là nghiệm của phương trình nào sau đây?

A. $n\left( n-1 \right)\left( n-2 \right)=720$

B. $n\left( n-1 \right)\left( n-2 \right)=120$

C. $n\left( n+1 \right)\left( n+2 \right)=120$

D. $n\left( n+1 \right)\left( n+2 \right)=720$

Câu 14:

Câu 14:

Cho hình chóp S.ABCD có đáy là hình vuông cạnh $a,SA\bot \left( ABCD \right),SA=a.$ Gọi G là trọng tâm tam giác ABD, khi đó khoảng cách từ điểm G đến mặt phẳng (SBC) bằng:

A. $\frac{a\sqrt{2}}{2}.$

B. $\frac{a\sqrt{2}}{3}.$

C. $\frac{a\sqrt{2}}{6}$

D. $\frac{a}{2}$

Câu 15:

Câu 15:

Tìm m để hàm số $y=\frac{1}{3}{{x}^{3}}-m{{x}^{2}}+\left( {{m}^{2}}-m+1 \right)x+1$ đạt cực đại tại $x=1.$

A. $\left[ \begin{align} & m=1 \\ & m=2 \\ \end{align} \right.$

B. $m=\pm 1$

C. $m=1$

D. $m=2$

Câu 16:

Câu 16:

Cho hình chóp S.ABCD có đáy là hình chữ nhật với $AB=2a,AD=a.$ Tam giác SAB là tam giác cân tại S và nằm trong mặt phẳng vuông góc với mặt đáy. Góc giữa mặt phẳng (SBC) và (ABCD) bằng 45°. Khi đó thể tích khối chóp S.ABCD là:

A. $\frac{\sqrt{3}{{a}^{3}}}{3}$

B. $\frac{2{{a}^{3}}}{3}$

C. $\frac{{{a}^{3}}}{3}$

D. $2{{a}^{3}}$

Câu 17:

Câu 17:

Đồ thị trong hình là của hàm số nào?

A. $y=-{{x}^{4}}+2{{x}^{2}}$

B. $y=-{{x}^{3}}+3x$

C. $y={{x}^{3}}-3x$

D. $y={{x}^{4}}-2{{x}^{2}}$

Câu 18:

Câu 18:

Xếp 10 quyển sách tham khảo khác nhau gồm: 1 quyển sách Văn, 3 quyển sách tiếng Anh và 6 quyển sách Toán thành một hàng ngang trên giá sách. Tính xác suất để mỗi quyển sách tiếng Anh đều được xếp ở giữa hai quyển sách Toán, đồng thời hai quyển Toán T1 và Toán T2 luôn được xếp cạnh nhau.

A. $\frac{1}{450}$

B. $\frac{1}{600}$

C. $\frac{1}{300}$

D. $\frac{1}{210}$

Câu 19:

Câu 19:

Tính thể tích V của khối lập phương ABCD.A'B'C'D'. Biết $AC'=a\sqrt{3}.$

A. $V=\frac{1}{3}{{a}^{3}}$

B. $V={{a}^{3}}$

C. $V=\frac{3\sqrt{6}{{a}^{3}}}{4}$

D. $3\sqrt{3}{{a}^{3}}$

Câu 20:

Câu 20:

Cho lăng trụ đứng tam giác ABC.A'B'C'. Biết tam giác ABC đều cạnh a và $AA'=a\sqrt{3}.$ Góc giữa hai đường thẳng AB' và mặt phẳng (A'B'C') bằng bao nhiêu?

A. 60°

B. 45°

C. 30°

D. 90°

Câu 21:

Câu 21:

Cho hàm số $y=\sqrt{3x-{{x}^{2}}}.$ Hàm số đồng biến trên khoảng nào?

A. $\left( 0;2 \right)$

B. $\left( 0;\frac{3}{2} \right)$

C. $\left( 0;3 \right)$

D. $\left( \frac{3}{2};3 \right)$

Câu 22:

Câu 22:

Cho hàm số $y={{x}^{3}}-\frac{3}{2}{{x}^{2}}+1.$ Gọi M là giá trị lớn nhất của hàm số trên $\left( -25;\frac{11}{10} \right).$ Tìm M.

A. $M=1.$

B. $M=\frac{1}{2}$

C. $M=0$

D. $M=\frac{129}{250}$

Câu 23:

Câu 23:

Biết đường thẳng $y=\left( 3m-1 \right)x+6m+3$ cắt đồ thị hàm số $y={{x}^{3}}-3{{x}^{2}}+1$ tại ba điểm phân biệt sao cho một giao điểm cách đều hai giao điểm còn lại. Khi đó m thuộc khoảng nào dưới đây?

A. $\left( 1;\frac{3}{2} \right)$

B. $\left( 0;1 \right)$

C. $\left( \frac{3}{2};2 \right)$

D. $\left( -1;0 \right)$

Câu 24:

Câu 24:

Cho hàm số $f\left( x \right)={{x}^{3}}-3{{x}^{2}}+1$. Có tất cả bao nhiêu giá trị nguyên của tham số m để hàm số $y=\left| f\left( \sin x+\sqrt{3}\cos x \right)+m \right|$ có giá trị nhỏ nhất không vượt quá 5?

A. 30

B. 32

C. 31

D. 29

Câu 25:

Câu 25:

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a, cạnh bên $SA=a\sqrt{5},$ mặt bên SAB là tam giác cân đỉnh S và thuộc mặt phẳng vuông góc với mặt phẳng đáy. Khoảng cách giữa hai đường thẳng AD và SC bằng:

A. $\frac{2a\sqrt{15}}{5}$

B. $\frac{a\sqrt{15}}{5}$

C. $\frac{4a\sqrt{5}}{5}$

D. $\frac{2a\sqrt{5}}{5}$

Câu 26:

Câu 26:

Cho hình chóp tam giác S.ABC có đáy ABC là tam giác đều cạnh a, cạnh bên SA vuông góc với đáy và $SA=2\sqrt{3}a.$ Tính thể tích V của khối chóp S.ABC.

A. $V=\frac{3{{a}^{3}}}{2}$

B. $V=\frac{3\sqrt{2}{{a}^{3}}}{2}$

C. $V={{a}^{3}}$

D. $V=\frac{{{a}^{3}}}{2}$

Câu 27:

Câu 27:

Gọi S là tập hợp các giá trị nguyên dương của m để hàm số $y={{x}^{3}}-3\left( 2m+1 \right){{x}^{2}}+\left( 12m+5 \right)x+2$ đồng biến trên khoảng $\left( 2;+\infty \right).$ Số phần tử của S bằng:

A. 1

B. 2

C. 3

D. 0

Câu 28:

Câu 28:

Cho hàm số $y=\frac{x-1}{x+1}$ có đồ thị là (C). Tiếp tuyến của (C) tại giao điểm của đồ thị với trục tung có phương trình là:

A. $x-2y-1=0$

B. $2x+y+1=0$

C. $x+2y+1=0$

D. $2x-y-1=0$

Câu 29:

Câu 29:

Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, cạnh bên hợp với đáy một góc 60°. Gọi M là điểm đối xứng của C qua D, N là trung điểm của SC. Mặt phẳng (BMN) chia khối chóp S.ABCD thành hai phần. Tỉ số thể tích giữa hai phần (phần lớn trên phần bé) bằng:

A. $\frac{7}{3}$

B. $\frac{7}{5}$

C. $\frac{1}{7}$

D. $\frac{6}{5}$

Câu 30:

Câu 30:

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Hai mặt bên (SAB) và (SAD) cùng vuông góc với mặt đáy. Biết góc giữa hai mặt phẳng (SCD) và (ABCD) bằng 45°. Gọi ${{V}_{1}};{{V}_{2}}$ lần lượt là thể tích khối chóp S.AHK và S.ACD với H, K lần lượt là trung điểm của SC và SD. Tính độ dài đường cao của khối chóp S.ABCD và tỉ số $k=\frac{{{V}_{1}}}{{{V}_{2}}}.$

A. $h=2a;k=\frac{1}{3}$

B. $h=a;k=\frac{1}{6}$

C. $h=2a;k=\frac{1}{8}$

D. $h=a;k=\frac{1}{4}$

Câu 31:

Câu 31:

Cho hình chóp tứ giác đều có cạnh đáy bằng $a$ và cạnh bên bằng $a\sqrt{3}.$ Tính thể tích $V$ của khối chóp đó theo $a.$

A. $V=\frac{{{a}^{3}}\sqrt{2}}{3}$

B. $V=\frac{{{a}^{3}}}{2}$

C. $V=\frac{{{a}^{3}}\sqrt{3}}{3}$

D. $V=\frac{{{a}^{3}}\sqrt{10}}{6}$

Câu 32:

Câu 32:

Cho hình chóp đều S.ABC có độ dài cạnh đáy bằng $a,$ cạnh bên bằng $a\sqrt{3}.$ Gọi O là tâm của đáy $ABC,{{d}_{1}}$ là khoảng cách từ A đến mặt phẳng (SBC) và ${{d}_{2}}$ là khoảng cách từ $O$ đến mặt phẳng (SBC). Tính $d={{d}_{1}}+{{d}_{2}}.$

A. $d=\frac{8a\sqrt{22}}{33}$

B. $d=\frac{2a\sqrt{22}}{33}$

C. $d=\frac{8a\sqrt{22}}{11}$

D. $d=\frac{2a\sqrt{22}}{11}$

Câu 33:

Câu 33:

Cho hàm số $y=\frac{2x+1}{x-1}.$ Đường tiệm cận đứng của đồ thị hàm số là:

A. Đường thẳng $x=1.$

B. Đường thẳng $x=2.$

C. Đường thẳng y = 2.

D. Đường thẳng y = 1.

Câu 34:

Câu 34:

Cho lăng trụ đứng ABC.A'B'C' có cạnh BC = 2a, góc giữa hai mặt phẳng (ABC) và (A'BC) bằng 60°. Biết diện tích tam giác A'BC bằng $2{{a}^{3}}.$ Tính thể tích khối lăng trụ ABC.A'B'C'.

A. $V=\frac{{{a}^{3}}\sqrt{3}}{3}$

B. $V=3{{a}^{3}}$

C. $V={{a}^{3}}\sqrt{3}$

D. $V=\frac{2{{a}^{3}}}{3}$

Câu 35:

Câu 35:

Tìm tất cả các giá trị của tham số $m$ để hàm số $y={{x}^{3}}-3{{x}^{2}}+mx$ đạt cực tiểu tại $x=2$?

A. $m\ne 0$

B. $m=0$

C. $m<0$

D. $m>0$

Câu 36:

Câu 36:

Cho hàm số $y=f\left( x \right)$ liên tục trên $\mathbb{R}$ và có bảng xét dấu của đạo hàm như hình vẽ. Hàm số đã cho có bao nhiêu điểm cực trị?

A. 4

B. 2

C. 3

D. 1

Câu 37:

Câu 37:

Số cạnh của một hình lăng trụ có thể là số nào dưới đây?

A. 2018

B. 2019

C. 2021

D. 2022

Câu 38:

Câu 38:

Số các giá trị của tham số $m$ để hàm số $y=\frac{x-{{m}^{2}}-1}{x-m}$ có giá trị lớn nhất trên [0;4] bằng $-6$ là:

A. 2

B. 1

C. 0

D. 3

Câu 39:

Câu 39:

Nhận định nào dưới đây là đúng?

A. Hàm số bậc ba có thể có một cực trị, hai cực trị hoặc không có cực trị nào.

B. Hàm số bậc ba có thể có hai cực trị hoặc không có cực trị nào.

C. Hàm số bậc ba có tối đa ba điểm cực trị.

D. Hàm số bậc ba có thể có một hoặc ba cực trị.

Câu 40:

Câu 40:

Tìm giá trị thực của tham số $m$ để đường thẳng $d:y=\left( 3m+1 \right)x+3+m$ vuông góc với đường thẳng đi qua hai điểm cực trị của đồ thị hàm số $y={{x}^{3}}-3{{x}^{2}}-1.$

A. $m=\frac{1}{6}$

B. $m=-\frac{1}{6}$

C. $m=\frac{1}{3}$

D. $m=-\frac{1}{3}$

Câu 41:

Câu 41:

Gọi S là tập hợp tất cả các giá trị nguyên của tham số $m$ để hàm số $y={{x}^{4}}-\left( {{m}^{2}}-9 \right){{x}^{2}}+2021$ có 1 cực trị. Số phần tử của tập S là:

A. Vô số

B. 3

C. 7

D. 5

Câu 42:

Câu 42:

Biết rằng đồ thị hàm số $y=\left( x-1 \right)\left( x+1 \right)\left( {{x}^{2}}-7 \right)-m$ cắt trục hoành tại 4 điểm phân biệt có hoành độ là ${{x}_{1}};{{x}_{2}};{{x}_{3}};{{x}_{4}}.$ Hỏi có tất cả bao nhiêu giá trị nguyên của tham số $m$ để $\frac{1}{1-{{x}_{1}}}+\frac{1}{1-{{x}_{2}}}+\frac{1}{1-{{x}_{3}}}+\frac{1}{1-{{x}_{4}}}>1?$

A. 9

B. 8

C. 6

D. 7

Câu 43:

Câu 43:

Cho hàm số $y=f\left( x \right)$ có đạo hàm liên tục trên khoảng K và có đồ thị là đường cong (C). Viết phương trình tiếp tuyến của (C) tại điểm $M\left( a;f\left( x \right) \right),\left( a\in K \right).$

A. $y'=f'\left( a \right)\left( x+a \right)+f\left( a \right)$

B. $y=f'\left( x \right)\left( x-a \right)+f\left( a \right)$

C. $y=f\left( a \right)\left( x-a \right)+f'\left( a \right)$

D. $y=f'\left( a \right)\left( x-a \right)-f\left( a \right)$

Câu 44:

Câu 44:

Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng $a$ và mặt bên tạo với đáy một góc 45°. Thể tích $V$ của khối chóp S.ABCD là:

A. $V=\frac{{{a}^{3}}}{6}$

B. $V=\frac{{{a}^{3}}}{9}.$

C. $V=\frac{{{a}^{3}}}{24}.$

D. $V=\frac{{{a}^{3}}}{2}$

Câu 45:

Câu 45:

Tìm tất cả các đường tiệm cận ngang của đồ thị hàm số $y=\frac{\left| x \right|}{\sqrt{{{x}^{2}}-1}}.$

A. $y=1;y=-1$

B. Không có tiệm cận ngang

C. $y=1$

D. $y=-1$

Câu 46:

Câu 46:

Cho hình hộp chữ nhật ABCD.A'B'C'D' có $AB=a,AD=b,AA'=c.$ Tính thể tích V của khối lăng trụ ABC.A'B'C'.

A. $V=abc$

B. $V=\frac{1}{6}abc$

C. $V=\frac{1}{2}abc$

D. $V=\frac{1}{3}abc$

Câu 47:

Câu 47:

Hàm số nào trong bốn hàm số sau có bảng biến thiên như hình vẽ sau?

A. $y=-{{x}^{3}}+3{{x}^{2}}-1$

B. $y={{x}^{3}}-3{{x}^{2}}+2$

C. $y={{x}^{3}}+3{{x}^{2}}-1$

D. $y={{x}^{3}}-3x+2$

Câu 48:

Câu 48:

Hàm số $y=\left| {{\left( x-1 \right)}^{3}}\left( x+1 \right) \right|$ có bao nhiêu điểm cực trị?

A. 3

B. 1

C. 2

D. 4

Câu 49:

Câu 49:

Cho hình lăng trụ tứ giác đều ABCD.A'B'C'D'. Biết $AC=2a$ và cạnh bên $AA'=a\sqrt{2}.$ Thể tích lăng trụ đó là:

A. $2\sqrt{2}{{a}^{3}}$

B. $\frac{4\sqrt{2}{{a}^{3}}}{3}$

C. $4\sqrt{2}{{a}^{3}}$

D. $\frac{2\sqrt{2}{{a}^{3}}}{3}$

Câu 50:

Câu 49:

Cho hình lăng trụ tứ giác đều ABCD.A'B'C'D'. Biết $AC=2a$ và cạnh bên $AA'=a\sqrt{2}.$ Thể tích lăng trụ đó là:

A. $2\sqrt{2}{{a}^{3}}$

B. $\frac{4\sqrt{2}{{a}^{3}}}{3}$

C. $4\sqrt{2}{{a}^{3}}$

D. $\frac{2\sqrt{2}{{a}^{3}}}{3}$