Đề thi thử THPT QG năm 2021 môn Toán online - Đề thi của Trường THPT Thành Nhân lần 2

Câu 1:

Thể tích của khối cầu bán kính $a$ bằng

Câu 2:

Với $a$ và $b$ là hai số thực dương tùy ý, $\log \left( a{{b}^{2}} \right)$ bằng

Câu 3:

Trong không gian Oxyz cho hai điểm $A\left( 2;3;4 \right)$ và $B\left( 3;0;1 \right)$. Khi đó độ dài vectơ $\overrightarrow{AB}$ là:

Câu 4:

Cho $\int\limits_{1}^{2}{f\left( x \right)dx}=2$ và $\int\limits_{1}^{2}{2g\left( x \right)dx}=8$. Khi đó $\int\limits_{1}^{2}{\left[ f\left( x \right)+g\left( x \right) \right]dx}$ bằng:

Câu 5:

Cho hàm số $f\left( x \right)$ có đồ thị như hình vẽ bên. Hàm số đã cho nghịch biến trên khoảng nào dưới đây?

Câu 6:

Tìm nghiệm của phương trình ${{\log }_{2}}\left( x-1 \right)=3.$

Câu 7:

Cho hàm số $y=f\left( x \right)$ liên tục trên $\mathbb{R}$ và có bảng biến thiên như hình vẽ:

Hàm số $y=f\left( x \right)$ là hàm số nào trong các hàm số sau:

Câu 8:

Trong không gian $Oxyz$, đường thẳng $d:\frac{x-1}{2}=\frac{y}{1}=\frac{z}{3}$ đi qua điểm nào dưới đây?

Câu 9:

Cho khối nón có độ dài đường sinh bằng 2a, góc giữa đường sinh và đáy bằng $60{}^\circ $. Thể tích của khối nón đã cho là:

Câu 10:

Trong không gian $Oxyz$, mặt phẳng $\left( Oxy \right)$ có phương trình là:

Câu 11:

Cho $\int\limits_0^1 {\left[ {f\left( x \right) – 2g\left( x \right)} \right]{\rm{d}}x} = 12$ và $\int\limits_0^1 {g\left( x \right){\rm{d}}x} = 5$, khi đó $\int\limits_0^1 {f\left( x \right){\rm{d}}x} $ bằng

Câu 12:

Thể tích của khối lăng trụ tam giác đều có cạnh đáy bằng a và độ dài cạnh bên bằng 2a là:

Câu 13:

Tìm công thức tính thể tích của khối tròn xoay khi cho hình phẳng giới hạn bởi parabol $\left( P \right):y={{x}^{2}}$ và đường thẳng d:y=2x quay xung quanh trục $Ox$.

Câu 14:

Tập nghiệm S của bất phương trình ${{5}^{x+2}}<{{\left( \frac{1}{25} \right)}^{-x}}$ là:

Câu 15:

Cho cấp số cộng $\left( {{u}_{n}} \right)$, biết ${{u}_{2}}=3$ và ${{u}_{4}}=7$. Giá trị của ${{u}_{2019}}$ bằng:

Câu 16:

Tìm điểm biểu diễn hình học của số phức $z=\frac{5}{2+i}$?

Câu 17:

Cho hàm số $y=f\left( x \right)$ có đồ thị như hình vẽ:

Số điểm cực trị của hàm số đã cho là:

Câu 18:

Họ nguyên hàm của hàm số $f\left( x \right)={{e}^{2x}}+{{x}^{2}}$ là:

Câu 19:

Tiếp tuyến của đồ thị hàm số $y=-{{x}^{3}}+3x-2$ tại điểm có hoành độ ${{x}_{0}}=2$ có phương trình là

Câu 20:

Tìm giá trị lớn nhất của hàm số $f\left( x \right)={{x}^{3}}-3{{x}^{2}}-9x+10$ trên $\left[ -2;\ 2 \right]$.

Câu 21:

Tập nghiệm của bất phương trình $2{{\log }_{2}}\left( x-1 \right)\le {{\log }_{2}}\left( 5-x \right)+1$ là:

Câu 22:

Cho khối chóp $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh a, SA vuông góc với mặt phẳng đáy và cạnh bên SB tạo với mặt phẳng đáy góc $45{}^\circ $. Thể tích của khối chóp $S.ABCD$ bằng:

Câu 23:

Biết ${{z}_{1}}$ và ${{z}_{2}}$ là 2 nghiệm của phương trình ${{z}^{2}}-4z+10=0$. Tính giá trị của biểu thức $T=\frac{{{z}_{1}}}{{{z}_{2}}}+\frac{{{z}_{2}}}{{{z}_{1}}}$.

Câu 24:

Đạo hàm của hàm số $y=x.{{e}^{x+1}}$ là:

Câu 25:

Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y=-{{x}^{4}}+2{{x}^{2}}-1$ trên đoạn $\left[ -2;1 \right]$. Tính $M+m$?

Câu 26:

Phương trình mặt cầu $\left( S \right)$ có tâm $I\left( 1;-2;3 \right)$ và tiếp xúc với mặt phẳng $\left( P \right):x-2y+2=0$ là:

Câu 27:

Cho hàm số $y=f\left( x \right)$ có đồ thị như hình vẽ:

Số nghiệm của phương trình $4{{f}^{2}}\left( x \right)-1=0$ là:

Câu 28:

Cho hình chóp S.ABC có đáy là tam giác vuông tại A có $AB=a\sqrt{3},\text{ }AC=a$, tam giác SBC đều và mặt trong mặt phẳng vuông góc với đáy (tham khảo hình vẽ). Góc giữa SA và mặt phẳng đáy là

Câu 29:

Cho hình lập phương $ABCD.\ A'B'C'D'$ với $O'$ là tâm hình vuông $A'B'C'D'$. Biết rằng tứ diện $O'BC\text{D}$có thể tích bằng $6{{a}^{3}}$. Tính thể tích V của khối lập phương $ABCD.\ A'B'C'D'$.

Câu 30:

Tập hợp các điểm biểu diễn số phức z thỏa mãn $\left| z-3i+1 \right|=4$ là:

Câu 31:

Cho hàm số $y=f\left( x \right)$ là hàm số xác định trên $\mathbb{R}\backslash \left\{ -1;1 \right\}$, liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau:

Số tiệm cận đứng của đồ thị hàm số là:

Câu 32:

Cho hàm số $y=f\left( x \right)$ liên tục trên $\mathbb{R}$ và có đồ thị như hình vẽ, diện tích hai phần ${{S}_{1}},{{S}_{2}}$ lần lượt bằng 12 và 3. Giá trị của $I=\int\limits_{-2}^{3}{f\left( x \right)dx}$ bằng:

Câu 33:

Trong không gian với hệ tọa độ $Oxyz$, hai điểm $A\left( 1;3;2 \right),B\left( 3;5;-4 \right)$. Phương trình mặt phẳng trung trực của AB là:

Câu 34:

Đường thẳng $\Delta $ là giao của hai mặt phẳng $\left( P \right):x+y-z=0$ và $\left( Q \right):x-2y+3=0$ thì có phương trình là:

Câu 35:

Cho hàm số $y=f\left( x \right)$ có đạo hàm là $f'\left( x \right)={{\left( x-2 \right)}^{4}}\left( x-1 \right)\left( x+3 \right)\sqrt{{{x}^{2}}+3}$. Tìm số điểm cực trị của hàm số $y=f\left( x \right)$:

Câu 36:

Cho hàm số $y=f'\left( x \right)$ liên tục trên $\mathbb{R}$ có đồ thị như hình vẽ bên cạnh và hàm số $\left( C \right):y=f\left( x \right)-\frac{1}{2}{{x}^{2}}-1$. Khẳng định nào sau đây là khẳng định sai?

Câu 37:

Trên giá sách có 4 quyển sách toán, 3 quyển sách lý, 2 quyển sách hóa. Lấy ngẫu nhiên 3 quyển sách. Tính xác suất để 3 quyển lấy ra thuộc 3 môn khác nhau.

Câu 38:

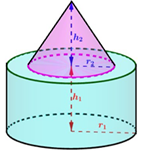
Một khối đồ chơi gồm một khối nón $\left( N \right)$ xếp chồng lên một khối trụ $\left( T \right)$. Khối trụ $\left( T \right)$ có bán kính đáy và chiều cao lần lượt là ${{r}_{1}},{{h}_{1}}$. Khối nón $\left( N \right)$ có bán kính đáy và chiều cao lần lượt là ${{r}_{2}},{{h}_{2}}$ thỏa mãn ${{r}_{2}}=\frac{2}{3}{{r}_{1}}$ và ${{h}_{2}}={{h}_{1}}$ (tham khảo hình vẽ bên). Biết rằng thể tích của toàn bộ khối đồ chơi bằng $124c{{m}^{3}}$, thể tích khối nón $\left( N \right)$ bằng:

Câu 39:

Cho $\int\limits_{0}^{1}{\frac{xdx}{{{\left( 2x+1 \right)}^{2}}}}=a+b\ln 2+c\ln 3$ với a, b, c là các số hữu tỉ. Giá trị của $a+b+c$ bằng:

Câu 40:

Cho hàm số $f\left( a \right)=\frac{{{a}^{\frac{2}{3}}}\left( \sqrt[3]{{{a}^{-2}}}-\sqrt[3]{a} \right)}{{{a}^{\frac{1}{8}}}\left( \sqrt[8]{{{a}^{3}}}-\sqrt[8]{{{a}^{-1}}} \right)}$ với $a>0,\,\,a\ne 1$. Giá trị của $M=f\left( {{2019}^{2018}} \right)$ là

Câu 41:

Cho hình chóp $S.ABCD$ có đáy là hình chữ nhật tâm $O,\ SD\bot \left( ABCD \right),AD=a$ và $\widehat{AOD}=60{}^\circ $. Biết SC tạo với đáy một góc $45{}^\circ $. Tính khoảng cách giữa hai đường thẳng AC và SB.

Câu 42:

Cho hàm số $y=f\left( x \right)$ thỏa mãn điều kiện $\int\limits_{0}^{2}{\frac{f'\left( x \right)dx}{x+2}}=3$ và $f\left( 2 \right)-2f\left( 0 \right)=4$. Tính tích phân $I=\int\limits_{0}^{1}{\frac{f\left( 2x \right)dx}{{{\left( x+1 \right)}^{2}}}}$.

Câu 43:

Trong không gian với hệ tọa độ $Oxyz$, phương trình nào dưới đây là phương trình hình chiếu của đường thẳng $d:\left\{ \begin{align}& x=-2t \\& y=t \\& z=-1-2t \\\end{align} \right.$ trên mặt phẳng $\left( P \right):x+y-z+1=0$.

Câu 44:

Cho phương trình $2\sqrt{{{\log }_{3}}\left( 3x \right)}-3{{\log }_{3}}x=m-1$ (với m là tham số thực). Có tất cả bao nhiêu giá trị nguyên dương của tham số m để phương trình trên có nghiệm?

Câu 45:

Đồ thị hàm số $y={{x}^{4}}-4{{x}^{2}}+2$ cắt đường thẳng $d:y=m$ tại 4 điểm phân biệt và tạo ra các hình phẳng có diện tích ${{S}_{1}},{{S}_{2}},{{S}_{3}}$ thỏa mãn ${{S}_{1}}+{{S}_{2}}={{S}_{3}}$ (như hình vẽ). Giá trị m thuộc khoảng nào sau đây?

Câu 46:

Cho hàm số $f\left( x \right)$ có bảng biến thiên như hình vẽ:

Số điểm cực trị của hàm số $g\left( x \right)={{\left[ f\left( {{x}^{2}} \right) \right]}^{2}}-3f\left( {{x}^{2}} \right)+1$ là:

Câu 47:

Trong không gian tọa độ $Oxyz$, cho mặt cầu $\left( S \right):{{\left( x-1 \right)}^{2}}+{{\left( y+1 \right)}^{2}}+{{z}^{2}}=\frac{5}{6}$, mặt phẳng $\left( P \right):x+y+z-1=0$ và điểm $A\left( 1;1;1 \right)$. Điểm M thay đổi trên đường tròn giao tuyến của $\left( P \right)$ và $\left( S \right)$. Giá trị lớn nhất của $P=AM$ là:

Câu 48:

Cho hàm số y = f(x) có đồ thị trên đoạn [-1;4] như hình vẽ bên. Số giá trị nguyên âm của tham số m để bất phương trình $m\ge f\left( \frac{x}{2}+1 \right)+{{x}^{2}}-4x$ có nghiệm trên đoạn [-1;4] là

Câu 49:

Xét các số phức z thỏa mãn $\left| z \right|=1$. Đặt $\text{w}=\frac{2\text{z}-i}{2+iz}$, giá trị lớn nhất của biểu thức $P=\left| \text{w}+3i \right|$ là

Câu 49:

Xét các số phức z thỏa mãn $\left| z \right|=1$. Đặt $\text{w}=\frac{2\text{z}-i}{2+iz}$, giá trị lớn nhất của biểu thức $P=\left| \text{w}+3i \right|$ là