Đề thi thử tốt nghiệp THPT môn Toán năm 2023 online - Đề thi của Trường THPT Vụ Bản

Câu 1:

Biết  $\int\limits_{1}^{2}{f\left( x \right)}\,dx=2$ và  $\int\limits_{1}^{5}{f\left( x \right)}\,dx=5$, khi đó  $\int\limits_{2}^{5}{f\left( x \right)dx}$ bằng

Câu 2:

Cho khối chóp có thể tích $4{{a}^{3}}$ và diện tích đáy $4{{a}^{2}}.$ Chiều cao của khối chóp đã cho bằng

Câu 3:

Cho hình phẳng giới hạn bởi đồ thị hàm số $y=\sin x$, trục $Ox$ và các đường thẳng $x=0,x=\pi $quay xung quanh $Ox.$ Thể tích khối tròn xoay tạo thành bằng

Câu 4:

Nguyên hàm của hàm số $f\left( x \right)=4x+\sin x$ là

Câu 5:

Cho hàm số $y=f\left( x \right)$ có bảng biến thiên như sau

Hàm số đã cho đồng biến trên khoảng nào dưới đây?

Câu 6:

Trong không gian $Oxyz,$ cho mặt cầu $\left( S \right):{{x}^{2}}+{{y}^{2}}+{{z}^{2}}-2x+4y-6z-5=0.$ Tâm của mặt cầu $\left( S \right)$ có tọa độ là

Câu 7:

Trong không gian $Oxyz,$ cho $\vec{a}=\left( 1;-2;3 \right)$ và $\vec{b}=\left( -1;3;0 \right)$. Vectơ $\vec{a}-\vec{b}$ có tọa độ là

Câu 8:

Cho khối lăng trụ tam giác có chiều cao $h=3$ và đáy là tam giác đều cạnh $a=2.$ Thể tích khối lăng trụ đã cho bằng

Câu 9:

Một cấp số cộng có hai số hạng liên tiếp là $-6$ và $4.$ Số hạng tiếp theo của cấp số cộng là

Câu 10:

Cho hình trụ có bán kính đáy $r=3$ và độ dài đường sinh $l=5.$ Diện tích xung quanh của hình trụ đã cho bằng  

Câu 11:

Cho hàm số $y=f\left( x \right)$ có bảng biến thiên như sau

Tiệm cận ngang của đồ thị hàm số là

Câu 12:

Tập nghiệm của bất phương trình ${{\log }_{0,5}}x+2\ge 0$ là

Câu 13:

Hàm số nào dưới đây có bảng biến thiên như hình sau

Câu 14:

Cho số thực $a$ thỏa mãn ${{a}^{3}}>{{a}^{\pi }}$. Mệnh đề nào sau đây đúng? 

Câu 15:

Cho hàm số $y=f\left( x \right)=a{{x}^{4}}+b{{x}^{2}}+c$  có  đồ thị như hình  vẽ bên. Số giá trị nguyên dương của tham số $m$ để phương trình $f\left( x \right)=m$ có hai nghiệm phân biệt là              

Câu 16:

Tập xác định của hàm số  $y={{\left( 9-{{x}^{2}} \right)}^{\frac{1}{3}}}+{{\left( x-2 \right)}^{-2}}$ là

Câu 17:

Với $a,b$ là các số thực dương tùy ý thỏa mãn ${{\log }_{3}}b-2{{\log }_{9}}a=2.$Mệnh đề nào dưới đây đúng?

Câu 18:

Một họa sĩ cần trưng bày $10$ bức tranh nghệ thuật khác nhau thành một hàng ngang. Hỏi có bao nhiêu cách để họa sĩ sắp xếp các bức tranh? 

Câu 19:

Cho hàm số bậc ba $y=f\left( x \right)$ có đồ thị là đường cong như hình vẽ bên. Điểm cực đại của đồ thị hàm số đã cho là

Câu 20:

Trong không gian $Oxyz,$ vectơ nào dưới đây là một vectơ pháp tuyến của mặt phẳng $\left( Oxy \right)?$

Câu 21:

Nghiệm của phương trình ${{2}^{1-3x}}=\frac{1}{32}$ là

Câu 22:

Cho hàm số $f\left( x \right)$ có bảng biến thiên như sau

Giá trị cực tiểu của hàm số $y=f\left( x \right)+1$ bằng 

Câu 23:

Trong không gian $Oxyz,$ cho hai điểm $A\left( 1;-2;5 \right)$ và $B\left( -2;-2;1 \right).$ Độ  dài đoạn thẳng $AB$ bằng 

Câu 24:

Cho khối nón có bán kính đáy $r=3$ và góc ở đỉnh bằng $60{}^\circ $.  Thể tích của khối nón giới hạn bởi hình nón đã cho bằng

Câu 25:

Đường cong trong hình vẽ bên là đồ thị hàm số nào trong bốn hàm số dưới đây?

Câu 26:

Biết $F\left( x \right)={{x}^{2}}$ là một nguyên hàm của hàm số $f\left( x \right)$ trên $\mathbb{R}$. Giá trị của $\int\limits_{1}^{3}{\left[ 2+f\left( x \right) \right]\text{d}x}$ bằng

Câu 27:

Trong các khẳng định sau, khẳng định nào sai?

Câu 28:

Đạo hàm của hàm số $y={{\log }_{3}}\left( 3x+1 \right)$ là

Câu 29:

Trong không gian $Oxyz,$ cho hai điểm $A\left( -2;0;1 \right)$ và $B\left( -2;2;-3 \right).$Mặt phẳng trung trực của đoạn thẳng AB có phương trình là

Câu 30:

Giá trị nhỏ nhất của hàm số $f\left( x \right)={{x}^{3}}-6x$ trên đoạn $\left[ -1;4 \right]$ là 

Câu 31:

Năm $2023$ một hãng xe niêm yết giá bán loại xe X là $750.000.000$ đồng và dự định trong $10$ năm tiếp theo, mỗi năm giảm $2%$ giá bán so với giá bán của năm liền trước. Theo dự định đó, năm $2030$ hãng xe ô tô niêm yết giá bán loại xe X là bao nhiêu? (kết quả làm tròn đến hàng nghìn)

Câu 32:

Số nghiệm của phương trình ${{\log }_{3}}\left( {{x}^{2}}+4x \right)$$ +{{\log }_{\frac{1}{3}}}\left( 3x+6 \right)=0$ là

Câu 33:

Cho hình hộp chữ nhật $ABCD.{A}'{B}'{C}'{D}'$ có $A{A}'=AD=a$, $AB=a\sqrt{2}$ (tham khảo hình vẽ). Góc giữa đường thẳng ${A}'C$ và mặt phẳng $\left( ABB'A' \right)$ bằng

Câu 34:

Cho hình chóp $S.ABC$ có $SA$ vuông góc với đáy, tam giác $ABC$ có $AB=a,$$AC=2a,\widehat{\,BAC}=120{}^\circ $ (tham khảo hình vẽ). Khoảng cách từ điểm $B$ đến mặt phẳng $\left( SAC \right)$ bằng

Câu 35:

Cho  hàm số $f\left( x \right)$  thỏa mãn $f'(x)=x.\cos 2x,\forall x\in \mathbb{R}$ và $f\left( 0 \right)=\frac{1}{4}.$ Hàm số $f\left( x \right)$ là  

Câu 36:

Cho hàm số $y=f(x)$ có đạo hàm ${f}'(x)=-x+2$ với mọi $x\in \mathbb{R}$. Hàm số đã cho nghịch biến trên khoảng nào dưới đây? 

Câu 37:

Trong không gian $Oxyz,$ cho hai điểm $A\left( 2;4;1 \right),B\left( -1;1;3 \right)$ và mặt phẳng $\left( P \right):x-3y+2z-5=0.$ Mặt phẳng $\left( Q \right)$ đi qua $A,B$ và vuông góc với $\left( P \right)$ có phương trình dạng $ax+by+cz+11=0.$ Tổng $a+b+c$ bằng 

Câu 38:

Gọi $S$ là tập hợp tất cả các số tự nhiên có ít nhất 3 chữ số và các chữ số đôi một khác nhau được lập từ các chữ số $1,2,3,4,5.$Chọn ngẫu nhiên hai số từ $S,$ tính xác xuất để hai số chọn được đều là số có ba chữ số.

Câu 39:

Có bao nhiêu giá trị nguyên của tham số $m$ để phương trình $\left( x-1 \right).\log \left( {{e}^{-x}}+m+2023 \right)=x-2$ có hai  nghiệm thực phân biệt? 

Câu 40:

Một ngọn hải đăng được đặt tại vị trí A cách bờ biển một khoảng $AB=5km.$ Trên bờ biển có một cái kho ở vị trí C cách  B  một khoảng $BC=7km$ (tham khảo hình vẽ). Người canh hải đăng có thể chèo đò từ vị trí  A  đến vị trí M  trên bờ biển với vận tốc $4\,km/h$ và đi bộ đến kho  C với vận tốc $6\,km/h.$ Hỏi muộn nhất mấy giờ người đó phải xuất phát từ vị trí  A  để có mặt ở kho C lúc 7 giờ sáng?

Câu 41:

Cho hàm số $f\left( x \right)$ liên tục trên $\mathbb{R}$ và thỏa mãn ${{x}^{2}}f\left( {{x}^{5}} \right)+xf\left( 1-{{x}^{4}} \right)=-3{{x}^{4}}+x+3,\,\forall x\in \mathbb{R}$. Khi đó $\int\limits_{0}^{1}{f\left( x \right)\text{d}x}$ bằng

Câu 42:

Trong không gian $Oxyz,$ cho mặt cầu $\left( S \right):{{x}^{2}}+{{y}^{2}}+{{\left( z-3 \right)}^{2}}=8$ và hai điểm $A\left( 4;-4;3 \right),$$B\left( 1;-1;7 \right).$ Gọi $\left( {{C}_{1}} \right)$ là tập hợp các điểm $M\in (S)$ sao cho  biểu thức $\left| MA-2MB \right|$ đạt giá trị nhỏ nhất.  Biết $\left( {{C}_{1}} \right)$ là một đường tròn, bán kính của đường tròn đó là

Câu 43:

Cho hình trụ có hai đáy là hình tròn tâm $O$ và ${O}'$, chiều cao $h=a\sqrt{3}$. Mặt phẳng đi qua tâm $O$ và tạo với $O{O}'$ một góc $30{}^\circ $, cắt hai đường tròn tâm $O$ và $O'$ tại bốn điểm là bốn đỉnh của một hình thang có đáy lớn gấp đôi đáy nhỏ và diện tích bằng $3{{a}^{2}}.$ Thể tích của khối trụ được giới hạn bởi hình trụ đã cho bằng

Câu 44:

Xét các số thực $x,y$thỏa mãn ${{2}^{{{x}^{2}}+{{y}^{2}}+1}}\le \left( {{x}^{2}}+{{y}^{2}}-2x+2 \right){{.4}^{x}}$. Giá trị lớn nhất của biểu thức $P=\frac{8x+4}{2x-y+1}$ gần nhất với số nào dưới đây

Câu 45:

Cho hàm số $f\left( x \right)$ có đạo hàm liên tục trên đoạn $\left[ 1;8 \right]$ và  thỏa mãn

                                       $\int\limits_{1}^{2}{{{\left[ f\left( {{x}^{3}} \right) \right]}^{2}}}dx+2\int\limits_{1}^{2}{f\left( {{x}^{3}} \right)}dx-\frac{4}{3}\int\limits_{1}^{8}{f\left( x \right)}dx=-\frac{247}{15}$.

Giả sử $F\left( x \right)$ là một nguyên hàm của hàm số $f\left( x \right)$ trên  đoạn $\left[ 1;8 \right].$Tích phân $\int\limits_{1}^{8}{xF'\left( x \right)}dx$ bằng

Câu 46:

Cho một tấm nhôm hình vuông cạnh $1\left( m \right)$ như hình vẽ bên.  

Người ta cắt phần tô đậm của tấm nhôm rồi gập thành một hình chóp tứ giác đều có cạnh đáy bằng $x\,\left( m \right)$ sao cho bốn đỉnh của hình vuông gập lại thành đỉnh của hình chóp. Giá trị của $x$ để khối chóp nhận được có thể tích lớn nhất là

Câu 47:

Cho hàm số bậc bốn $f\left( x \right)=a{{x}^{4}}+b{{x}^{3}}+c{{x}^{2}}+dx+e\ \left( a,b,c,d,e\in \mathbb{R} \right)$ và hàm số bậc ba $g\left( x \right)=m{{x}^{3}}+n{{x}^{2}}+px+q\ \left( m,n,p,q\in \mathbb{R} \right)$ có đồ thị $y=f'\left( x \right)$ và $y=g'\left( x \right)$ như hình vẽ bên dưới.

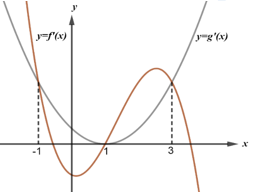
Biết diện tích hình phẳng giới hạn bởi hai đồ thị hàm số $y=f\left( x \right)$ và $y=g\left( x \right)$ bằng 96  và $f\left( 2 \right)=g\left( 2 \right)$. Diện tích hình phẳng giới hạn bởi các đường $y=f\left( x \right),y=g\left( x \right)$ và $x=0,\ x=2$ bằng

Câu 48:

Cho hàm số $f\left( x \right)$ biết  hàm số $y={{f}'}'(x)$ là hàm đa thức bậc bốn có đồ thị như hình vẽ bên.

Đặt $g(x)=2f\left( \frac{1}{2}{{x}^{2}} \right)+f\left( -{{x}^{2}}+6 \right)$, biết rằng $g(0)>0$ và $g\left( 2 \right)<0.$ Số điểm cực tiểu của hàm số $y=\left| g\left( x \right) \right|$ là

Câu 49:

Trong không gian $Oxyz,$ cho hai điểm $A\left( -10;6;-2 \right),B\left( -5;10;-9 \right)$ và mặt phẳng $\left( \alpha  \right):2x-2y-z+12=0$. Điểm $M\left( a;b;c \right)$ thuộc $\left( \alpha  \right)$ sao cho $MA,MB$  tạo với $\left( \alpha  \right)$ các góc bằng nhau và biểu thức $T=2M{{A}^{2}}-M{{B}^{2}}$ đạt giá trị nhỏ nhất. Tổng $a+b+c$ bằng

Câu 49:

Trong không gian $Oxyz,$ cho hai điểm $A\left( -10;6;-2 \right),B\left( -5;10;-9 \right)$ và mặt phẳng $\left( \alpha  \right):2x-2y-z+12=0$. Điểm $M\left( a;b;c \right)$ thuộc $\left( \alpha  \right)$ sao cho $MA,MB$  tạo với $\left( \alpha  \right)$ các góc bằng nhau và biểu thức $T=2M{{A}^{2}}-M{{B}^{2}}$ đạt giá trị nhỏ nhất. Tổng $a+b+c$ bằng